Simulación de ondas en 2D

Agustín Alayón González

Simulación de propagación de ondas en diferentes condiciones

Introducción:

Se planteara la simulación de una onda o serie de ondas en una y dos dimensiones en presencia de obstáculos diversos, para ello se empleará un programa realizado en C++, se podrá observar de diferentes modos, ya que se puede presentar diferentes opciones para una visualización mas adecuada, de acuerdo a las necesidades del estudio.

Descripción de propagación

Consideremos una función ξ = f(x), representada gráficamente por la curva continua de la fig 1. Si reemplazamos x por x – a, obtenemos la función ξ=f(x-a). Evidentemente, la forma de la curva no ha cambiado: los mismos valores de ξ se obtienen para valores de x aumentados en a. En otras palabras, suponiendo que a es positiva, vemos que la curva ha sido desplazada sin deformación, hacia la derecha, una cantidad a. Análogamente tenemos que ξ = f(x+a) corresponde a un desplazamiento rígido de la curva hacia la izquierda, en la cantidad a.

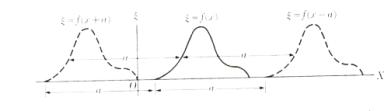
Si a =vt, donde te es el tiempo, obtenemos una curva “viajera”; esto es, ξ=f(x-vt) representa una curva que se mueve hacia la derecha con velocidad v, llamada velocidad de fase (fig 2ª) Del mismo modo , ξ = f(x + vt) representa una curva que se mueve hacia la izquierda con velocidad v (fig 2b). Con lo que se concluye una expresión matemática de forma ξ(x,t) = f(x ± vt) es adecuada para describir una situación física que “viaja” o se propaga” sin deformación en la dirección del eje X; esto se llama movimiento ondulatorio. La cantidad ξ(x,t) puede representar muy diversas cantidades físicas, tales como la deformación de un sólido, la presión de un gas, el campo magnético, etc.

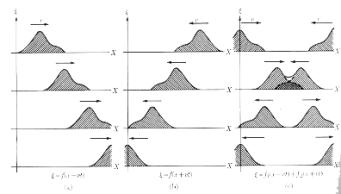
A continuación se investiga como determinar cuando un campo dado, en función del tiempo, se propaga como una onda sin distorsión. Como los campos asociados con cada proceso físico están gobernados por las leyes dinámicas (características de cada proceso) que pueden expresarse en la forma de ecuaciones diferenciales, como se puede mostrar en el caso del campo electromagnético, debemos explorar la posibilidad de encontrar una ecuación diferencial que sea aplicable a todo tipo de movimiento ondulatorio. Entonces, cada vez que reconozcamos que un campo particular, como resultado de sus propiedades físicas, satisface tal ecuación, podemos estar seguros que el mismo se propaga a través del espacio con velocidad definida sin distorsión. Recíprocamente, si experimentalmente observamos que un campo se propaga a través del espacio con una velocidad definida y sin distorsión, estamos en condiciones de describir tal campo por medio de un conjunto de ecuaciones compatibles con la ecuación de onda.

La ecuación que encontraremos muchas veces y que describe un movimiento ondulatorio que se propaga a una velocidad definida v y sin distorsión según las direcciones +X ó –X es

(1)

Ondas superficiales en un líquido.

Las ondas más comunes son las que podemos observar en el mar o en el océano, en lagos, o simplemente las que se producen en un pozo cuando cae una piedra en él. El aspecto matemático, sin embargo, es mas complicado por el que trataremos de observarlo con la simulación que en se tratará. La superficie de un liquido en equilibrio es plana y horizontal. Una perturbación de la superficie produce un desplazamiento de todas las moléculas situadas inmediatamente debajo de la superficie. Fig 1. Cada volumen elemental de líquido describe una trayectoria cerrada. La amplitud de los desplazamientos vertical y horizontal de un elemento de volumen de un fluido varia, en general, con la profundidad. Desde luego, las moléculas del fondo no experimentan desplazamiento vertical, porque no pueden separarse del mismo. En la superficie del líquido entran en juego ciertas fuerzas además de la fuerza debida a la presión atmosférica. Una de ellas es la debida a la tensión superficial del líquido, que da lugar a una fuerza hacia arriba sobre el elemento de superficie, similar a la que se encuentra en el caso de una cuerda. Otra fuerza es el peso del líquido situado por encima del nivel de equilibrio. La ecuación resultante para el desplazamiento de la superficie no es exactamente del tipo (1), sino ligeramente más complicada. Sin embargo, es satisfecha por las armónicas de longitud de onda λ y velocidad de propagación dada por:

(2)

Donde ρ es la densidad del liquido, T la tensión superficial y g la aceleración de la gravedad. Esta ecuación es válida para profanidades no muy grandes en comparación con la longitud de onda λ. En caso contrario, la expresión resultante es diferente.

El aspecto más interesante de la ecuación anterior, es que la velocidad de propagación depende de la longitud de onda. Como la frecuencia está relacionada con la longitud de onda y con la velocidad de propagación a través de ν = υ / λ, concluimos que la velocidad de propagación depende de la frecuencia. Supongamos, por ejemplo, que λ es suficientemente grande como para que el segundo término de la ecuación sea despreciable. Entonces tenemos.

(3)

Las ondas en este caso son llamadas en este caso, ondas gravitacionales. Con esta aproximación la velocidad de propagación es independiente de la naturaleza del líquido, ya que ningún factor referente al líquido (tal como su densidad o tensión superficial) aparece en la ecuación (3), Vemos que, en este caso, la velocidad de propagación es proporcional a la raíz cuadrada de la longitud de onda, y que a mayor longitud de onda, mayor rapidez de propagación. Por esta razón un viento fuerte y continuado produce ondas de mayor longitud de onda que una ráfaga repentina e irregular.

Cuando la longitud de onda es muy pequeña, el término que predomina es el segundo en la ecuación (2) y entonces la velocidad de propagación es

(4)

Estas ondas se llaman rizado y ondas capilares; son las ondas que se observan cuando sopla una brisa, o cuando el recipiente que contiene un liquido se somete a vibraciones de alta frecuencia y pequeña amplitud. En este caso, a mayor amplitud de onda, menor velocidad de propagación.

Cuando la velocidad de propagación de un movimiento ondulatorio depende de la longitud de onda o de la frecuencia, decimos que hay dispersión. Si un movimiento ondulatorio resultante de la superposición de varias ondas armónicas de diferentes frecuencias penetra en un medio dispersivo, la onda se distorsiona por que cada una de sus ondas componentes se propaga con diferente velocidad. La dispersión es un fenómeno importante que se presenta en varios tipos de propagación de ondas. En particular las ondas electromagnéticas a través de la materia.

Para nuestro caso, la simulación de las ondas vamos a usar dos programas similares, el primero el que va a representar ondas de propagación en una dimensión, el cual se va a dividir en; propagación de un frente de ondas, y propagación de un pulso de ondas. El segundo programa se tratará de un programa de un frente de ondas indefinido y en el que se podrá observa el comportamiento en diferentes circunstancias.

Programas

Para la realización del programa se ha usado lo siguiente:

1. El programa se ha escrito en C++ y se ha usado como soporte OpenGL y las librerias FOX para GUI donde se usa para la interfase

2. Se realiza una solución parcial de las ecuaciones diferenciales de ondas

3. se usa una conversión simple para obtener ecuaciones de primer orden

Para el de 1D:

Se usa el glut program, en el que usa la representación de las imágenes con OpenGL, los pulsos de ondas se activan automáticamente al abrir el programa, y se pueden generar sucesivos pulsos con solo pulsar la barra espaciadora.

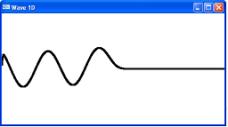
Para el caso de propagación de 2D, el programa empleado resulta mas completo, en el se tiene diferentes opciones:

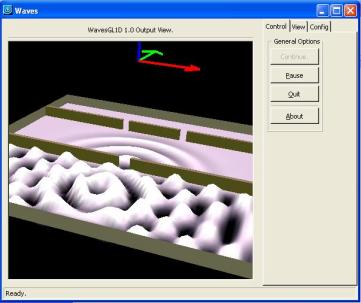
En la primera pantalla tenemos las opciones de Control, en el se definen las siguientes opciones:

Continue à Esta activada cuando el programa esta corriendo.

Pause à Detiene la ejecución del programa.

Quit à Sale del programe en cuestión.

About à Especifica los autores del programa

Maciej Matyka

ul. Kielczowska 137/10

51-315 Wroclaw

Poland

http://panoramix.ift.uni.wroc.pl/~maq

maq@panoramix.ift.uni.wroc.pl

En la segunda pantalla (View), nos encontramos con los siguientes opciones:

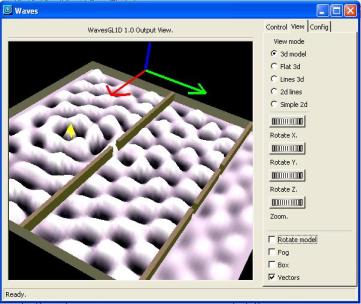
Las opciones de View mode, hace referencia a las opciones de proyección, estas pueden ser:

. 3d model : modo normal, en el que generalmente nos vamos a basar.

. Flat 3d : Las imágenes se muestran planas, es decir, sin sombras.

. Lines 3d: En este caso se muestran líneas.

. Lines 2d: Misma representación a la anterior, pero en este caso, la vista se realiza desde el eje z, con lo cual tenemos una visión en 2d .

. Simple 2d: Realiza una visión de las zonas donde se producen los antinodos siendo estas más claras, en la dirección positiva del eje z, y oscuras en la dirección negativa.

. Rotate : Amplia o aleja la imagen para una mejor observación, y rota esta en los diferentes ejes.

. Rotate model: Rota el modelo de forma automática en torno al eje z (solo es activo para los parámetros en 3d).

. Fog : Oscurece la imagen.

. Box: Activa las paredes del recinto de estudio.

. Vectors: Activa/desactiva los vectores (x,y,z)

3ª pantalla

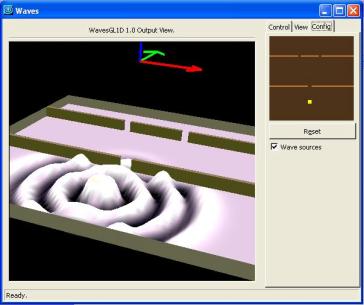
En esta pantalla tenemos la configuración del modelo que queremos estudiar.

El cuadro marrón, representa la zona de configuración, donde podemos colocar las diversas fuentes así como diversas barreras. Estas se pueden realizar con el ratón (botón primario = barrera/s ; botón secundario = fuente/s)

Reset à Elimina todas las opciones puestas.

Waves sources à Activa, si la fuente es continua o solo un frente de ondas.

Desarrollo:

Supongamos primeramente una onda de 1 dimensión propagándose en linea recta en dirección de izquierda a derecha, en un recinto cerrado de dimensión L, como se muestra en la figura, la onda inicia su propagación

Cuando esta llegue al punto L (donde se encuentra el final de la cuerda) esta sufrirá una reflexión. De forma como se puede apreciar en la siguiente figura.

Si la reflexión esta en fase con la onda incidente se producirá una onda con suma de amplitudes formando una onda constructiva (como es el caso mostrado), mientras que si la onda no están en fase, la suma de ondas será destructiva, y no se apreciara onda alguna.

Como se muestra en la figura anterior se ve que las sumas de ondas son destructivas.

Si se deja progresar las ondas en un tiempo, se puede apreciar que las ondas cuando sufren múltiples reflexiones

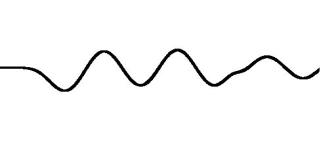
Vemos que después pasado las ondas reflejadas el frente de onda inicial, se aprecia que las ondas que reflejan son idénticas a las originales (ondas de la izquierda)

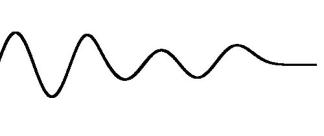
Imagen mostrada después de múltiples reflexiones

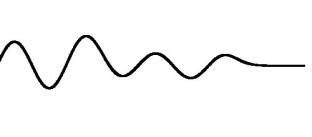
Si no hay perdidas de energía de disipación, se aprecia que para tiempos largos, las ondas van reduciendo amplitud, para aumentar el ancho de banda. Fourier hace un analisis de esta situación en el que se demuestra que ΔxΔk ≈ 2π por lo tanto se sigue conservando la energía, y el frente de ondas continuará con sucesivas reflexiones.

Esta deducción se puede demostrar en la siguiente simulación, en donde se aplica un pulso de onda que viaja de izquierda a derechas, y cuyas reflexiones se muestran de forma invertida.

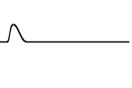
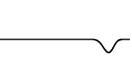
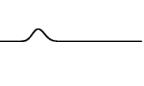
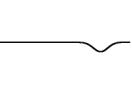
Como se aprecia, tenemos una serie de reflexiones (3 en nuestro caso) y se aprecia como se conserva lo predicho por el análisis de Fourier. Si continuasemos con el procedimiento, se llegaria a una onda con una achura muy grande, y una amplitud muy pequeña que casi se muestra inapreciable en nuestro caso.

Ondas 2D

Pasemos a continuación a una onda en dos dimensiones. En el caso que vamos a estudiar es el caso de una o varias fuentes de ondas, las cuales producen un paquete de ondas indefinidas y a su vez vemos también como estas se propagan. También se observará como se comporta esta cuando se encuentre con una serie de obstáculos.

· . Primeramente se va a considerar una sola fuente de onda dentro de un recinto cerrado [AAG1] . Esta suposición será para el resto de las experiencias

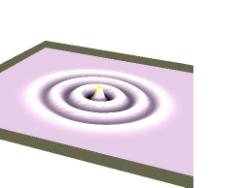
Para ello consideramos la onda situado en el centro del recinto, vemos como la onda se propaga en todas las direcciones.

Al cabo de un cierto tiempo y considerando que las distancias de los extremos del recinto son próximas para considerar que las pérdidas de energía de las ondas son despreciables, tenemos que estas sufren una reflexión, enfrentándose a las ondas incidentes de forma que queda de la siguiente forma:

Se puede apreciar que a diferencias de la imagen anterior, que ya las ondas no son círculos perfectos en propagación. Esto se debe a la interferencia de las ondas incidentes y reflejadas, en esta se produce la interferencia constructiva, donde se aprecia que sobresalen unos máximos (en nuestro caso se aprecian con unos picos mayores), e interferencia destructivas (donde se ve que la suma de ambas ondas produce una zona donde se ve un hueco).

Cuando estas continúan propagándose en ambas direcciones se presenta el siguiente:

Se puede apreciar que la distribución de ondas constructivas y destructivas ha alcanzado la mayor parte del recinto, y con más detalle se perciben las interferencias constructivas y destructivas.

Imagen de las ondas después de un periodo largo, en el que las ondas han sufrido unas series de reflexiones diversas, se ve que en todo el recinto hay una interferencias de ondas

Cuando el tiempo es suficientemente largo, las ondas se convierten en estacionarias

Presentando la imagen que se observa.

Para dos fuentes de ondas:

El problema que se planteara será de forma similar al ejercicio anterior, en este caso ya las interferencias no se producirá en las paredes del recinto, sino que se producirá también en las ondas de la fuente contigua como se podrá apreciar en las siguientes imágenes

Como se aprecia, la interferencia es de forma similar que en el caso de una sola fuente, pero en esta ocasión la interferencia se produce con mayor rapidez, esto es debido a que una de la fuente de onda respecto a la otra, hace que actúe como en el caso anterior como reflexión en la pared, es decir, cuando en el planteamiento anterior las interferencias se producía después de sufrir las ondas reflexiones en la pared, ahora las ondas sufren reflexiones constructivas y destructivas, por la interferencias de las ondas de la fuente contigua.

Se aprecia que después de un tiempo suficientemente largo, la interferencia se produce en todo el recinto, y por tanto tendremos ondas constructivas como destructivas.

3 ondas:

Como se demuestra, el proceso es idéntico a los casos anteriores, y actúa de forma similar, tanto al primer caso como al segundo caso. Por lo que se puede anticipar que para sucesivas fuentes dentro del recinto, el procedimiento que va a experimentar será idéntico. Lo que diferencia los distintos casos, es que el tiempo de interacción entre ondas será mas rápido, y esto es debido a lo que se comento en el caso de dos fuentes de ondas, que la interacción de las ondas de las fuentes vecinas hará producir una interacción de ondas mas rápidamente actuando estas como ondas de reflexión.

Lo que se planteara después de observar como se comporta una serie de ondas dentro de un recinto. Lo que plantearemos a continuación es como esta se comporta cuando se enfrenta a una serie de obstáculos.

Frente de ondas en un obstáculo

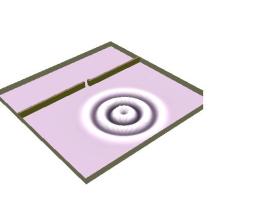
En un comienzo, y considerando una única fuente, tenemos que el frente de ondas aún no se ha percatado del obstáculo.

Después de llegar a este, la onda sufre en la zona donde se encuentra la pared con los mismos procedimientos que en los casos anteriores. Pero en el lugar donde aparece la abertura, la onda se convertirá como nuevo frente de ondas, como se podrá observar en las imágenes siguientes:

Por lo tanto tendremos la fuente de ondas original, que se observa como la zona marcada en amarillo, y después una fuente creada por el frente de ondas que llegan a la abertura.

Vemos como se presenta el frente de ondas producido por la abertura.

Cuando esta misma situación se produce, pero con una abertura mayor, se puede comprobar que el comportamiento es similar

Como se puede observar, a medida que la anchura de la abertura aumenta, esta se comporta como nueva fuente de ondas, pero con la peculiaridad de que las ondas son planas, y proporcionales a la anchura de esta.

Se observa con mayor detalle lo anteriormente dicho.

De forma más compleja, se puede observar que se producen nuevos frentes de ondas. Así de forma sucesiva, este efecto se sigue conservando.

Conclusión.

Queda demostrado como se produce los efectos de onda, así de forma visual, se puede comprobar este comportamiento, ya que a diferencia de las formas teóricas, se puede observar como se forma los antinodos, también se pueden apreciar como se producen los nuevos frentes de ondas, cuando esta se encuentra con una barrera con una abertura.

A diferencias lo presentado en este informe, se pueden construir múltiples posibilidades, el cual omitimos y que se deja a estudio del interesado.