Volume Calculation (Gauss Theorem)

A mathematical expression which describe Gauss theorem can be written in following form:

$$\int\int\int_V (\vec{\nabla} \cdot \vec{F}) d\tau = \oint_S \vec{F} d\vec{s}$$ (7)

Where $\vec{F}$ is a vector field, $V$ is whole body volume and $S$ is body surface. Let us rewrite it in a case of two dimensional object:

$$\int\int_V (\vec{\nabla} \cdot \vec{F}) d\tau = \oint_L \vec{F} d\vec{l}$$ (8)

Where $V$ is body field, $\vec{F}$ is any vector field and $L$ is body edge. If we assume $\vec{F} = (x,0)$ then because of:

$$\vec{\nabla} \cdot \vec{F} = 1$$ (9)

and

$$\vec{F} \cdot d\vec{l} = (x,0) \cdot \hat{n} \cdot dl = x \cdot n_x\cdot dl$$ (10)

we will get a simple expression which describe body field value (our "volume" calculated in the code):

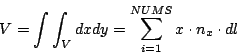$$V = \int\int_V dxdy = \sum_{i=1}^{NUMS} x \cdot n_x\cdot dl$$ (11)