Volume of The Body

In the paper [1] we introduced simple technique for calculation of soft objects volume Bounding objects are simple and straighforward way to do it. You simply define $x_{min}, x_{max}$ and $y_{min}, y_{max}$ of all body points, the bounding box (rectangle in two dimensions) gives you first approximation of the body volume. When I had a talk on SIGRAD'03 conference in UMEA (Sweden), after my talk Jos Stam⁹ told me that he know easy way to fast calculation of the volume of the body. Yeah.. almost 5 years of physics studies and I forgot about Gauss theorem - it was in my head when he told me this idea. Idea is simple, but you need to have some knowledge in academic math. If you heard about Gauss theorem - with closed shapes we are able to replace integration over volume by integration over surface of the body. In one of appendixes you will find more formal derivation of an idea of the body integration.

However for our purposes we use simply expression for body volume¹⁰:

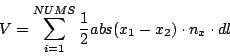$$V = \sum_{i=1}^{NUMS} \frac{1}{2}abs(x_1 - x_2) \cdot n_x \cdot dl$$ (3)

where: $V$ is body volume, $abs(x_1 - x_2)$ is an absolute difference of $x$ component of the spring start and end points, $n_x$ is normal vector $x$ component and finally $dl$ is spring length. We do a sum over all springs in the model (sum from $i=1$ to $NUMS$), since spring is a model of an edge in that model. Implementation of that procedure is very easy and straighforward, that simple loop is presented below.

/* Calculate Volume of the Ball 
(Gauss Theorem) */

for(i=1 ; i<=NUMS-1 ; i++)
{
  x1 = myPoints[ mySprings[i].i ].x;	
  y1 = myPoints[ mySprings[i].i ].y;
  x2 = myPoints[ mySprings[i].j ].x;	
  y2 = myPoints[ mySprings[i].j ].y;

  // calculate sqr(distance)
 r12d = sqrt ( 
         (x1 - x2) *(x1 - x2) +  
         (y1 - y2) * (y1 - y2) );  

  volume += 0.5 * fabs(x1 - x2) * 
          fabs(mySprings[i].nx) * (r12d);

    }

Now we have done two steps of pressure force calculation. Normal vector calculation and volume of the body calculation. What we have left is to calculate final force and distribute it over all points in the model.